Ruby Hacking Guide
Translated by Vincent ISAMBART & ocha-
Chapter 9: yacc crash course
Outline
Parser and scanner
How to write parsers for programming languages has been an active area of research for a long time, and there is a quite firm established tactic for doing it. If we limit ourselves to a grammar not too strange (or ambiguous), we can solve this problem by following this method.
The first part consists in splitting a string in a list of words (or tokens). This is called a scanner or lexer. The term “lexical analyzer” is also used, but is too complicated to say so we’ll use the name scanner.
When speaking about scanners, the common sense first says “there are generally spaces at the end of a word”. And in practice, it was made like this in most programming languages, because it’s the easiest way.
There can also be exceptions. For example, in the old Fortran, white spaces did not have any meaning. This means a white space did not end a word, and you could put spaces in the name of a variable. However that made the parsing very complicated so the compiler vendors, one by one, started ignoring that standard. Finally Fortran 90 followed this trend and made the fact that white spaces have an impact the standard.
By the way, it seems the reason white spaces had not meaning in Fortran 77 was that when writing programs on punch cards it was easy to make errors in the number of spaces.
List of symbols
I said that the scanner spits out a list of words (tokens), but, to be exact, what the scanner creates is a list of “symbols”, not words.
What are symbols? Let’s take numbers as an example. In a programming language, 1, 2, 3, 99 are all “numbers”. They can all be handled the same way by the grammar. Where we can write 1, we can also write 2 or
- That’s why the parser does not need to handle them in different ways. For numbers, “number” is enough.
“number”, “identifier” and others can be grouped together as
“symbol”. But be careful not to mix this with the Symbol class.
The scanner first splits the string into words and determines what
these symbols are. For example, NUMBER or DIGIT for numbers,
IDENTIFIER for names like “name”, IF for the reserved word
if. These symbols are then given to the next phase.
Parser generator
The list of words and symbols spitted out by the scanner are going to be used to form a tree. This tree is called a syntax tree.
The name “parser” is also sometimes used to include both the scanner and the creation of the syntax tree. However, we will use the narrow sense of “parser”, the creation of the syntax tree. How does this parser make a tree from the list of symbols? In other words, on what should we focus to find the tree corresponding to a piece of code?
The first way is to focus on the meaning of the words. For example,
let’s suppose we find the word var. If the definition of the local
variable var has been found before this, we’ll understand it’s the
reading of a local variable.
An other ways is to only focus on what we see. For example, if after
an identified comes a ‘=’, we’ll understand it’s an assignment. If
the reserved word if appears, we’ll understand it’s the start of an
if statement.
The later method, focusing only on what we see, is the current trend. In other words the language must be designed to be analyzed just by looking at the list of symbols. The choice was because this way is simpler, can be more easily generalized and can therefore be automatized using tools. These tools are called parser generators.
The most used parser generator under UNIX is yacc. Like many others,
ruby’s parser is written using yacc. The input file for this tool
is parser.y. That’s why to be able to read ruby’s parser, we need
to understand yacc to some extent. (Note: Starting from 1.9, ruby
requires bison instead of yacc. However, bison is mainly yacc
with additional functionality, so this does not diminish the interest
of this chapter.)
This chapter will be a simple presentation of yacc to be able to
understand parse.y, and therefore we will limit ourselves to what’s
needed to read parse.y. If you want to know more about parsers and
parser generators, I recommend you a book I wrote called “Rubyを256倍使
うための本 無道編” (The book to use 256 times more of Ruby -
Unreasonable book). I do not recommend it because I wrote it, but
because in this field it’s the easiest book to understand. And besides
it’s cheap so stakes will be low.
Nevertheless, if you would like a book from someone else (or can’t read Japanese), I recommend O’Reilly’s “lex & yacc programming” by John R. Levine, Tony Mason and Doug Brown. And if your are still not satisfied, you can also read “Compilers” (also known as the “dragon book” because of the dragon on its cover) by Alfred V. Aho, Ravi Sethi and Jeffrey D. Ullman.
Grammar
Grammar file
The input file for yacc is called “grammar file”, as it’s the file
where the grammar is written. The convention is to name this grammar
file *.y. It will be given to yacc who will generate C source
code. This file can then be compiled as usual (figure 1 shows the full
process).
The output file name is always y.tab.c and can’t be changed. The
recent versions of yacc usually allow to change it on the command
line, but for compatibility it was safer to keep y.tab.c. By the
way, it seems the tab of y.tab.c comes from table, as lots of
huge tables are defined in it.
It’s good to have a look at the file once.
The grammar file’s content has the following form:
▼ General form of the grammar file
%{
Header
%}
%union ....
%token ....
%type ....
%%
Rules part
%%
User defined part
yacc’s input file is first divided in 3 parts by %%. The first
part if called the definition part, has a lot of definitions and
setups. Between %{ and %} we can write anything we want in C, like
for example necessary macros. After that, the instructions starting
with % are special yacc instructions. Every time we use one, we’ll
explain it.
The middle part of the file is called the rules part, and is the most
essential part for yacc. It’s where is written the grammar we want
to parse. We’ll explain it in details in the next section.
The last part of the file, the user defined part, can be used freely
by the user. yacc just copies this part verbatim in the output
file. It’s used for example to put auxiliary routines needed by the
parser.
What does yacc do.
What yacc takes care of is mainly this rules part in the
middle. yacc takes the grammar written there and use it to make a
function called yyparse(). It’s the parser, in the narrow sense of
the word.
In the narrow sense, so it means a scanner is needed. However, yacc
won’t take care of it, it must be done by the user.
The scanner is the function named yylex().
Even if yacc creates yyparse(), it only takes care of its core
part. The “actions” we’ll mention later is out of its scope. You can
think the part done by yacc is too small, but that’s not the
case. That’s because this “core part” is overly important that yacc
survived to this day even though we keep complaining about it.
But what on earth is this core part? That’s what we’re going to see.
BNF
When we want to write a parser in C, its code will be “cut the string
this way, make this an if statement…” When using parser
generators, we say the opposite, that is “I would like to parse this
grammar.” Doing this creates for us a parser to handle the
grammar. This means telling the specification gives us the
implementation. That’s the convenient point of yacc.
But how can we tell the specification? With yacc, the method of
description used is the BNF (Backus-Naur Form). Let’s look at a very
simple example.
if_stmt: IF expr THEN stmt END
Let’s see separately what’s at the left and at the right of the
“:”. The part on the left side, if_stmt, is equal to the right
part… is what I mean here. In other words, I’m saying that:
if_stmt and IF expr THEN stmt END are equivalent.
Here, if_stmt, IF, expr… are all “symbols”. expr is the
abbreviation of expression, stmt of statement. It must be for
sure the declaration of the if statement.
One definition is called a rule. The part at the left of “:” is
called the left side and the right part called the right side. This is
quite easy to remember.
But something is missing. We do not want an if statement without
being able to use else. And even if we could write else, having
to always write the else even when it’s useless would be
cumbersome. In this case we could do the following:
if_stmt: IF expr THEN stmt END
| IF expr THEN stmt ELSE stmt END
”|” means “or”.
if_stmt is either “IF expr THEN stmt END” or “IF expr THEN stmt
ELSE stmt END”.
That’s it.
Here I would like you to pay attention to the split done with
|. With just this, one more rule is added. In fact, punctuating with
| is just a shorter way to repeat the left side. The previous
example has exactly the same meaning as the following:
if_stmt: IF expr THEN stmt END
if_stmt: IF expr THEN stmt ELSE stmt END
This means two rules are defined in the example.
This is not enough to complete the definition of the if
statement. That’s because the symbols expr and stmt are not sent
by the scanner, their rules must be defined. To be closer to Ruby, let’s
boldly add some rules.
stmt : if_stmt
| IDENTIFIER '=' expr /* assignment */
| expr
if_stmt: IF expr THEN stmt END
| IF expr THEN stmt ELSE stmt END
expr : IDENTIFIER /* reading a variable */
| NUMBER /* integer constant */
| funcall /* FUNction CALL */
funcall: IDENTIFIER '(' args ')'
args : expr /* only one parameter */
I used two new elements. First, comments of the same form as in C, and
character expressed using '='. This '=' is also of course a
symbol. Symbols like “=” are different from numbers as there is only
one variety for them. That’s why for symbols where can also use '='.
It would be great to be able to use for strings for, for example,
reserved words, but due to limitations of the C language this cannot
be done.
We add rules like this, to the point we complete writing all the
grammar. With yacc, the left side of the first written rule is “the
whole grammar we want to express”. So in this example, stmt
expresses the whole program.
It was a little too abstract. Let’s explain this a little more
concretely. By “stmt expresses the whole program”, I mean stmt and
the rows of symbols expressed as equivalent by the rules, are all
recognized as grammar. For example, stmt and stmt are
equivalent. Of course. Then expr is equivalent to stmt. That’s
expressed like this in the rule. Then, NUMBER and stmt are
equivalent. That’s because NUMBER is expr and expr is stmt.
We can also say that more complicated things are equivalent.
stmt
↓
if_stmt
↓
IF expr THEN stmt END
↓ ↓
IF IDENTIFIER THEN expr END
↓
IF IDENTIFIER THEN NUMBER END
When it has expanded until here, all elements become the symbols sent by the scanner. It means such sequence of symbols is correct as a program. Or putting it the other way around, if this sequence of symbols is sent by the scanner, the parser can understand it in the opposite order of expanding.
IF IDENTIFIER THEN NUMBER END
↓
IF IDENTIFIER THEN expr END
↓ ↓
IF expr THEN stmt END
↓
if_stmt
↓
stmt
And stmt is a symbol expressing the whole program. That’s why this
sequence of symbols is a correct program for the parser. When it’s the
case, the parsing routine yyparse() ends returning 0.
By the way, the technical term expressing that the parser succeeded is that it “accepted” the input. The parser is like a government office: if you do not fill the documents in the boxes exactly like he asked you to, he’ll refuse them. The accepted sequences of symbols are the ones for which the boxes where filled correctly. Parser and government office are strangely similar for instance in the fact that they care about details in specification and that they use complicated terms.
Terminal symbols and nonterminal symbols
Well, in the confusion of the moment I used without explaining it the expression “symbols coming from the scanner”. So let’s explain this. I use one word “symbol” but there are two types.
The first type of the symbols are the ones sent by the scanner. They
are for example, IF, THEN, END, '=', … They are called
terminal symbols. That’s because like before when we did the quick
expansion we find them aligned at the end. In this chapter terminal
symbols are always written in capital letters. However, symbols like
'=' between quotes are special. Symbols like this are all terminal
symbols, without exception.
The other type of symbols are the ones that never come from the
scanner, for example if_stmt, expr or stmt. They are called
nonterminal symbols. As they don’t come from the scanner, they only
exist in the parser. Nonterminal symbols also always appear at one
moment or the other as the left side of a rule. In this chapter,
nonterminal symbols are always written in lower case letters.
How to test
I’m now going to tell you the way to process the grammar file with
yacc.
%token A B C D E
%%
list: A B C
| de
de : D E
First, put all terminal symbols used after %token. However, you do
not have to type the symbols with quotes (like '='). Then, put %%
to mark a change of section and write the grammar. That’s all.
Let’s now process this.
% yacc first.y
% ls
first.y y.tab.c
%
Like most Unix tools, “silence means success”.
There’s also implementations of yacc that need semicolons at the end
of (groups of) rules. When it’s the case we need to do the following:
%token A B C D E
%%
list: A B C
| de
;
de : D E
;
I hate these semicolons so in this book I’ll never use them.
Void rules
Let’s now look a little more at some of the established ways of grammar description. I’ll first introduce void rules.
void:
There’s nothing on the right side, this rule is “void”. For example,
the two following targets means exactly the same thing.
target: A B C
target: A void B void C
void :
What is the use of such a thing? It’s very useful. For example in the following case.
if_stmt : IF expr THEN stmts opt_else END
opt_else:
| ELSE stmts
Using void rules, we can express cleverly the fact that “the else
section may be omitted”. Compared to the rules made previously using
two definitions, this way is shorter and we do not have to disperse
the burden.
Recursive definitions
The following example is still a little hard to understand.
list: ITEM /* rule 1 */
| list ITEM /* rule 2 */
This expresses a list of one or more items, in other words any of the following lists of symbols:
ITEM
ITEM ITEM
ITEM ITEM ITEM
ITEM ITEM ITEM ITEM
:
Do you understand why? First, according to rule 1 list can be read
ITEM. If you merge this with rule 2, list can be ITEM ITEM.
list: list ITEM
= ITEM ITEM
We now understand that the list of symbols ITEM ITEM is similar to
list. By applying again rule 2 to list, we can say that 3 ITEM
are also similar to list. By quickly continuing this process, the
list can grow to any size.
This is something like mathematical induction.
I’ll now show you the next example. The following example expresses
the lists with 0 or more ITEM.
list:
| list ITEM
First the first line means “list is equivalent to (void)”. By void I
mean the list with 0 ITEM. Then, by looking at rule 2 we can say
that “list ITEM” is equivalent to 1 ITEM. That’s because list is
equivalent to void.
list: list ITEM
= (void) ITEM
= ITEM
By applying the same operations of replacement multiple times, we can
understand that list is the expression a list of 0 or more items.
With this knowledge, “lists of 2 or more ITEM” or “lists of 3 or
more ITEM” are easy, and we can even create “lists of an even number
of elements”.
list:
| list ITEM ITEM
Construction of values
This abstract talk lasted long enough so in this section I’d really like to go on with a more concrete talk.
Shift and reduce
Up until now, various ways to write grammars have been explained, but what we want is being able to build a syntax tree. However, I’m afraid to say, only telling it the rules is not enough to be able to let it build a syntax tree, as might be expected. Therefore, this time, I’ll tell you the way to build a syntax tree by adding something to the rules.
We’ll first see what the parser does during the execution. We’ll use the following simple grammar as an example.
%token A B C
%%
program: A B C
In the parser there is a stack called the semantic stack. The parser pushes on it all the symbols coming from the scanner. This move is called “shifting the symbols”.
[ A B ] ← C shift
And when any of the right side of a rule is equal to the end of the stack, it is “interpreted”. When this happens, the sequence of the right-hand side is replaced by the symbol of the left-hand side.
[ A B C ]
↓ reduction
[ program ]
This move is called “reduce A B C” to program”. This term
is a little presumptuous, but in short it is like,
when you have enough number of tiles of haku and hatsu and chu respectively,
it becomes “Big three dragons” in Japanese Mahjong,
… this might be irrelevant.
And since program expresses the whole program,
if there’s only a program on the stack, it probably means the whole program is
found out. Therefore, if the input is just finished here, it is accepted.
Let’s try with a little more complicated grammar.
%token IF E S THEN END
%%
program : if
if : IF expr THEN stmts END
expr : E
stmts : S
| stmts S
The input from the scanner is this.
IF E THEN S S S END
The transitions of the semantic stack in this case are shown below.
| Stack | Move |
| empty at first | |
IF |
shift IF |
IF E |
shift E |
IF expr |
reduce E to expr |
IF expr THEN |
shift THEN |
IF expr THEN S |
shift S |
IF expr THEN stmts |
reduce S to stmts |
IF expr THEN stmts S |
shift S |
IF expr THEN stmts |
reduce stmts S to stmts |
IF expr THEN stmts S |
shift S |
IF expr THEN stmts |
reduce stmts S to stmts |
IF expr THEN stmts END |
shift END |
if |
reduce IF expr THEN stmts END to if |
program |
reduce if to program |
| accept. |
As the end of this section, there’s one thing to be cautious with. a reduction does not always means decreasing the symbols. If there’s a void rule, it’s possible that a symbol is generated out of “void”.
Action
Now, I’ll start to describe the important parts.
Whichever shifting or reducing,
doing several things only inside of the semantic stack is not meaningful.
Since our ultimate goal was building a syntax tree,
it cannot be sufficient without leading to it.
How does yacc do it for us?
The answer yacc made is that “we shall enable to hook the moment when the
parser performing a reduction.” The hooks are called actions of the parser.
An action can be written at the last of the rule as follows.
program: A B C { /* Here is an action */ }
The part between { and } is the action. If you write like this,
at the moment reducing A B C to program this action will be executed.
Whatever you do as an action is free.
If it is a C code, almost all things can be written.
The value of a symbol
This is further more important but,
each symbol has “its value”.
Both terminal and nonterminal symbols do.
As for terminal symbols, since they come from the scanner,
their values are also given by the scanner.
For example, 1 or 9 or maybe 108 for a NUMBER symbol.
For an IDENTIFIER symbol, it might be "attr" or "name" or "sym".
Anything is fine.
Each symbol and its value are pushed together on the semantic stack.
The next figure shows the state just the moment S is shifted with its value.
IF expr THEN stmts S
value value value value value
According to the previous rule, stmts S can be reduced to stmts.
If an action is written at the rule, it would be executed,
but at that moment, the values of the symbols corresponding to the right-hand
side are passed to the action.
IF expr THEN stmts S /* Stack */
v1 v2 v3 v4 v5
↓ ↓
stmts: stmts S /* Rule */
↓ ↓
{ $1 + $2; } /* Action */
This way an action can take the value of each symbol corresponding to the
right-hand side of a rule through $1, $2, $3, …
yacc will rewrite the kinds of $1 and $2 to the notation to point to the stack.
However because it is written in C language it needs to handle, for instance,
types, but because it is tiresome, let’s assume their types are of int for the moment.
Next, instead it will push the symbol of the left-hand side, but because all
symbols have their values the left-hand side symbol must also have its value.
It is expressed as $$ in actions, the value of $$ when leaving an action
will be the value of the left-hand side symbol.
IF expr THEN stmts S /* the stack just before reducing */
v1 v2 v3 v4 v5
↓ ↓
stmts: stmts S /* the rule that the right-hand side matches the end */
↑ ↓ ↓
{ $$ = $1 + $2; } /* its action */
IF expr THEN stmts /* the stack after reducing */
v1 v2 v3 (v4+v5)
As the end of this section, this is just an extra. The value of a symbol is sometimes called “semantic value”. Therefore the stack to put them is the “semantic value stack”, and it is called “semantic stack” for short.
yacc and types
It’s really cumbersome but without talking about types we cannot finish this
talk. What is the type of the value of a symbol?
To say the bottom line first, it will be the type named YYSTYPE.
This must be the abbreviation of either YY Stack TYPE or Semantic value TYPE.
And YYSTYPE is obviously the typedef of somewhat another type.
The type is the union defined with the instruction named %union in the definition part.
We have not written %union before but it did not cause an error. Why?
This is because yacc considerately process with the default value without asking.
The default value in C should naturally be int.
Therefore, YYSTYPE is int by default.
As for an example of a yacc book or a calculator, int can be used unchanged.
But in order to build a syntax tree,
we want to use structs and pointers and the other various things.
Therefore for instance, we use %union as follows.
%union {
struct node {
int type;
struct node *left;
struct node *right;
} *node;
int num;
char *str;
}
Because this is not for practical use,
the arbitrary names are used for types and members.
Notice that it is different from the ordinal C but there’s no semicolon at the
end of the %unicon block.
And, if this is written, it would look like the following in y.tab.c.
typedef union {
struct node {
int type;
struct node *left;
struct node *right;
} *node;
int num;
char *str;
} YYSTYPE;
And, as for the semantic stack,
YYSTYPE yyvs[256]; /* the substance of the stack(yyvs = YY Value Stack) */
YYSTYPE *yyvsp = yyvs; /* the pointer to the end of the stack */
we can expect something like this. Therefore, the values of the symbols appear in actions would be
/* the action before processed by yacc */
target: A B C { func($1, $2, $3); }
/* after converted, its appearance in y.tab.c */
{ func(yyvsp[-2], yyvsp[-1], yyvsp[0]); ;
naturally like this.
In this case, because the default value int is used,
it can be accessed just by referring to the stack.
If YYSTYPE is a union, it is necessary to also specify one of its members.
There are two ways to do that, one way is associating with each symbol,
another way is specifying every time.
Generally, the way of associating with each type is used.
By using %token for terminal symbols and
using %type for nonterminal symbols,
it is written as follows.
%token<num> A B C /* All of the values of A B C is of type int */
%type<str> target /* All of the values of target is of type char* */
On the other hand, if you’d like to specify everytime,
you can write a member name into next to $ as follows.
%union { char *str; }
%%
target: { $<str>$ = "In short, this is like typecasting"; }
You’d better avoid using this method if possible.
Defining a member for each symbol is basic.
Coupling the parser and the scanner together
After all, I’ve finished to talk all about this and that of the values inside the parser. For the rest, I’ll talking about the connecting protocol with the scanner, then the heart of this story will be all finished.
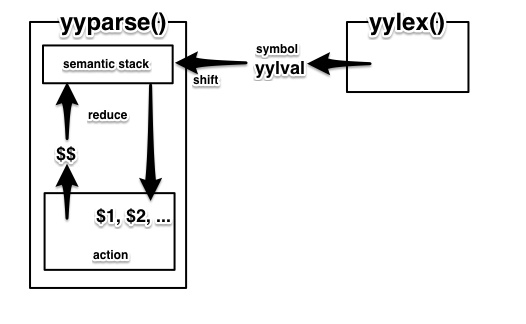
First, we’d like to make sure that I mentioned that the scanner was the yylex() function.
each (terminal) symbol itself is returned (as int) as a return value of the function.
Since the constants with the same names of symbols are defined (#define) by
yacc, we can write NUMBER for a NUMBER.
And its value is passed by putting it into a global variable named yylval.
This yylval is also of type YYSTYPE,
and the exactly same things as the parser can be said.
In other words, if it is defined in %union it would become a union.
But this time the member is not automatically selected,
its member name has to be manually written.
The very simple examples would look like the following.
static int
yylex()
{
yylval.str = next_token();
return STRING;
}
Figure 2 summarizes the relationships described by now.
I’d like you to check one by one.
yylval, $$, $1, $2 …
all of these variables that become the interfaces are of type YYSTYPE.
yacc related variables & functionsEmbedded Action
An action is written at the last of a rule, is how it was explained. However, actually it can be written in the middle of a rule.
target: A B { puts("embedded action"); } C D
This is called “embedded action”.
An embedded action is merely a syntactic sugar of the following definition:
target: A B dummy C D
dummy : /* void rule */
{
puts("embedded action");
}
From this example, you might be able to tell everything including
when it is executed.
The value of a symbol can also be taken.
In other words, in this example,
the value of the embedded action will come out as $3.
Practical Topics
Conflicts
I’m not afraid of yacc anymore.
If you thought so, it is too naive.
Why everyone is afraid so much about yacc,
the reason is going to be revealed.
Up until now, I wrote not so carefully “when the right-hand side of the rule matches the end of the stack”, but what happens if there’s a rule like this:
target : A B C
| A B C
When the sequence of symbols A B C actually comes out,
it would be hard to determine which is the rule to match.
Such thing cannot be interpreted even by humans.
Therefore yacc also cannot understand this.
When yacc find out an odd grammar like this,
it would complain that a reduce/reduce conflict occurs.
It means multiple rules are possible to reduce at the same time.
% yacc rrconf.y
conflicts: 1 reduce/reduce
But usually, I think you won’t do such things except as an accident.
But how about the next example?
The described symbol sequence is completely the same.
target : abc
| A bc
abc : A B C
bc : B C
This is relatively possible. Especially when each part is complicatedly moved while developing rules, it is often the case that this kind of rules are made without noticing.
There’s also a similar pattern, as follows:
target : abc
| ab C
abc : A B C
ab : A B
When the symbol sequence A B C comes out,
it’s hard to determine whether
it should choose one abc or the combination of ab and C.
In this case, yacc will complain that a shift/reduce conflict occurs.
This means there’re both a shift-able rule and a reduce-able rule
at the same time.
% yacc srconf.y
conflicts: 1 shift/reduce
The famous example of shift/reduce conflicts is “the hanging else problem”.
For example, the if statement of C language causes this problem.
I’ll describe it by simplifying the case:
stmt : expr ';'
| if
expr : IDENTIFIER
if : IF '(' expr ')' stmt
| IF '(' expr ')' stmt ELSE stmt
In this rule,
the expression is only IDENTIFIER (variable),
the substance of if is only one statement.
Now, what happens if the next program is parsed with this grammar?
if (cond)
if (cond)
true_stmt;
else
false_stmt;
If it is written this way, we might feel like it’s quite obvious. But actually, this can be interpreted as follows.
if (cond) {
if (cond)
true_stmt;
}
else {
false_stmt;
}
The question is
“between the two ifs, inside one or outside one,
which is the one to which the else should be attached?”.
However shift/reduce conflicts are relatively less harmful than reduce/reduce
conflicts, because usually they can be solved by choosing shift.
Choosing shift is almost equivalent to “connecting the elements closer to each
other” and it is easy to match human instincts.
In fact, the hanging else can also be solved by shifting it.
Hence, the yacc follows this trend,
it choses shift by default when a shift/reduce conflict occurs.
Look-ahead
As an experiment,
I’d like you to process the next grammar with yacc.
%token A B C
%%
target : A B C /* rule 1 */
| A B /* rule 2 */
We can’t help expecting there should be a conflict.
At the time when it has read until A B,
the rule 1 would attempt to shift,
the rule 2 would attempt to reduce.
In other words, this should cause a shift/reduce conflict. However, ….
% yacc conf.y
%
It’s odd, there’s no conflict. Why?
In fact, the parser created with yacc can look ahead only one symbol.
Before actually doing shift or reduce,
it can decide what to do by peeking the next symbol.
Therefore, it is also considered for us when generating the parser,
if the rule can be determined by a single look-ahead,
conflicts would be avoided.
In the previous rules, for instance, if C comes right after A B,
only the rule 1 is possible and it would be chose (shift).
If the input has finished, the rule 2 would be chose (reduce).
Notice that the word “look-ahead” has two meanings:
one thing is the look-ahead while processing *.y with yacc.
The other thing is the look-ahead while actually executing the generated parser.
The look-ahead during the execution is not so difficult,
but the look-ahead of yacc itself is pretty complicated.
That’s because
it needs to predict all possible input patterns and decides its behaviors
from only the grammar rules.
However, because “all possible” is actually impossible,
it handles “most of” patterns.
How broad range over all patterns it can cover up shows
the strength of a look-ahead algorithm.
The look-ahead algorithm that yacc uses when processing grammar files is
LALR(1), which is relatively powerful among
currently existing algorithms to resolve conflicts.
A lot things have been introduced, but you don’t have to so worry because what to do in this book is only reading and not writing. What I wanted to explain here is not the look-ahead of grammars but the look-ahead during executions.
Operator Precedence
Since abstract talks have lasted for long, I’ll talk more concretely.
Let’s try to define the rules for infix operators such as + or *.
There are also established tactics for this, we’d better tamely follow it.
Something like a calculator for arithmetic operations is defined below:
expr : expr '+' expr
| expr '-' expr
| expr '*' expr
| expr '/' expr
| primary
primary : NUMBER
| '(' expr ')'
primary is the smallest grammar unit.
The point is that expr between parentheses becomes a primary.
Then, if this grammar is written to an arbitrary file and compiled, the result would be this.
% yacc infix.y
16 shift/reduce conflicts
They conflict aggressively. Thinking for 5 minutes is enough to see that this rule causes a problem in the following and similar cases:
1 - 1 - 1
This can be interpreted in both of the next two ways.
(1 - 1) - 1
1 - (1 - 1)
The former is natural as an numerical expression.
But what yacc does is the process of their appearances,
there does not contain any meanings.
As for the things such as the meaning the - symbol has,
it is absolutely not considered at all.
In order to correctly reflect a human intention,
we have to specify what we want step by step.
Then, what we can do is writing this in the definition part.
%left '+' '-'
%left '*' '/'
These instructions specifies both the precedence and the associativity
at the same time.
I’ll explain them in order.
I think that the term “precedence” often appears when talking about the grammar of a programming language. Describing it logically is complicated, so if I put it instinctively, it is about to which operator parentheses are attached in the following and similar cases.
1 + 2 * 3
If * has higher precedence, it would be this.
1 + (2 * 3)
If + has higher precedence, it would be this.
(1 + 2) * 3
As shown above, resolving shift/reduce conflicts by defining the stronger ones and weaker ones among operators is operator precedence.
However, if the operators has the same precedence, how can it be resolved? Like this, for instance,
1 - 2 - 3
because both operators are -, their precedences are the completely same.
In this case, it is resolved by using the associativity.
Associativity has three types: left right nonassoc,
they will be interpreted as follows:
| Associativity | Interpretation |
| left (left-associative) | (1 - 2) - 3 |
| right (right-associative) | 1 - (2 - 3) |
| nonassoc (non-associative) | parse error |
Most of the operators for numerical expressions are left-associative.
The right-associative is used mainly for = of assignment and not of denial.
a = b = 1 # (a = (b = 1))
not not a # (not (not a))
The representatives of non-associative are probably the comparison operators.
a == b == c # parse error
a <= b <= c # parse error
However, this is not the only possibility. In Python, for instance, comparisons between three terms are possible.
Then, the previous instructions named %left %right %noassoc are used to
specify the associativities of their names.
And, precedence is specified as the order of the instructions.
The lower the operators written, the higher the precedences they have.
If they are written in the same line, they have the same level of precedence.
%left '+' '-' /* left-associative and third precedence */
%left '*' '/' /* left-associative and second precedence */
%right '!' /* right-associative and first precedence */